Angle of view of a vintage camera
Angle of view (AOV) describes the angular extent of a given scene that is imaged by a camera.
Derivation
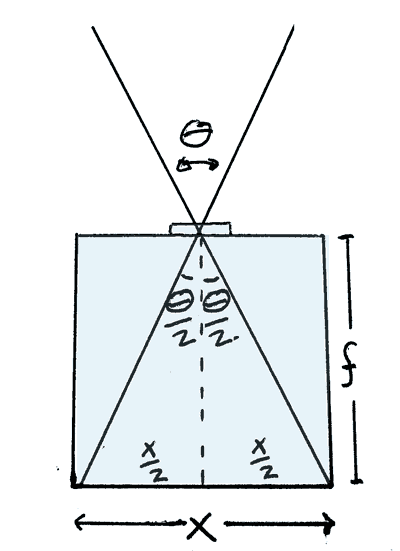
From diagram
Assuming camera is focussed on infinity
θ/2= arctan((X/2)/f))
so
Angle of View(θ)=2*arctan(X/2f)
where X is a distance on the image plane
and f is the focal length of the lens.
X can be the width, height or diagonal of the film plane.
Arctan is often shown as tan-1 on calculators.
Note that the angle of view varies slightly when the focus is not at infinity. This is because the lens is moved forward slightly to focus closer. This only becomes an issue with macro photography.
Typical Angle of View
Most single lens vintage cameras have an angle of view similar to the human eye which is about 55 degrees. This angle of view for a camera would give a perspective in a photograph that would be similar to the scene viewed with the naked eye.
Example 1 - Beau Brownie
The Beau Brownie No.2 camera uses 120 film. When used in landscape mode it has an image width on the film plane of 3¼ inches (82mm). The focal length of the Beau Brownie is 85mm.
The angle of view is therefore θ=2*arctan(82/(2*85)) = 51.5 degrees.
Example 2 - Kodak Bantam Special
The Kodak Bantam Special uses 828 film. When used in landscape mode it has an image width on the film plane of 40mm. The focal length of the Bantam is 45mm.
The angle of view is therefore θ=2*arctan(40/(2*45)) = 48 degrees.
The Diagonal
The values quoted for cameras are often related to the diagonal of the image. For the Beau Brownie this gives an angle of view of 60.6 degrees and for the Bantam it gives an angle of view of 57 degrees.
Field of View
The field of view is the width of the field at a particular distance(d).
Field of View (FOV) = 2 * d * tan (θ/2)
Example
The field of view for a Beau Brownie at the distance of 20 m is:-
FOV = 2 * 20 * tan(51.5/2°) = 40 * tan(25.75°) = 19.3 m